Source- Dribbble
There are numerous data sources that can be used for navigation, including GPS, WiFi, Bluetooth® LE protocols and many more. Among them is inertial navigation, one of the most precise sources of information for indoor positioning.
How does an inertial navigation system work?
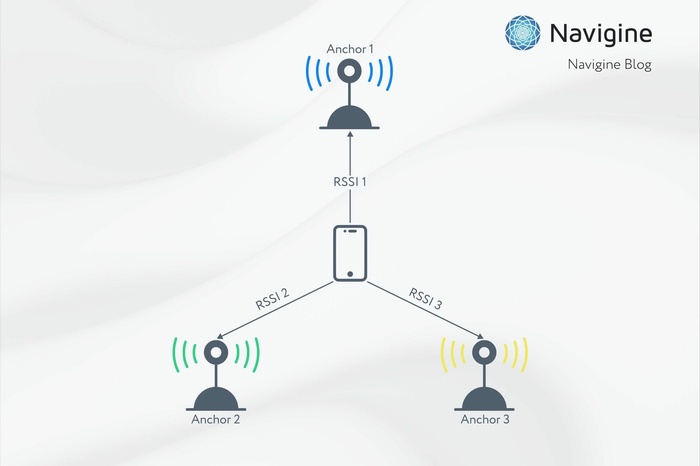
Inertial navigation system includes devices, data processing techniques and computational algorithms that allow to determine position of a certain navigation unit in space and time. The Inertial measurement unit (IMU) that is used by Navigine consists of an accelerometer, gyroscope and magnetometer. These sensors can be installed on most modern mobile devices. They can detect rotation, shaking and swiping of a user. Signals from these devices can be processed simultaneously all together or separately if one of them is not available. To well incorporate data from these different measurement sources It is necessary to apply filtration mechanisms. Navigine uses algorithms that are based on complementary filter for data processing and smoothing the results.
Accelerometer
The accelerometer measures the acceleration force and provides measurements in 3D space. The most common accelerometers are designed to use three one dimensional accelerometers, one for each direction. Both magnetometer and gyroscope acquire data in three dimensions, but all the navigation is performed in only two dimensions. That is why an accelerometer is crucial to determine the direction of gravity force. Measurements from other sensors can be projected to the surface, perpendicular to the gravity vector.

Figure accel

Figure “Accelerometer”
Pedometer
Pedometer detects pics of acceleration magnitude. When the user stands still, acceleration almost remains constant, but not equal to zero because of the existence of gravity force. During motion specific patterns can be observed. It helps to detect moments of steps. Before analyzing signals it is necessary to apply preprocessing to measurements because some of them can be considered as noise. The incoming signals can be cleaned using a low-pass filter and adjusted to the value of gravitational acceleration. Step detection is performed using step threshold. The moment when acceleration goes beyond the threshold is considered as the beginning of the step. When acceleration goes below the threshold, the end of the step is recorded. Step length can be calculated by combining the information about acceleration in the beginning and end of step, time spent on one step, total time and total distance.

Picture “Noise filtering and gravity value adjustment” from this video.
Gyroscope
Gyroscope measures angular rate using the Coriolis effect. Depending on the type of gyroscope, it assesses the force generated by rotation of the device. The rotation angle is integrated over time to provide change in the orientation on a specific time interval. Gyroscope gives a more accurate estimated heading in a short-term navigation period compared to magnetometer. However, when it comes to long time intervals the gyroscope is less precise because of accumulation of the error during the integration process.

Figure gyro

Picture this
Magnetometer
This sensor measures the Earth magnetic field by using magneto-resisting effect or Hall effect. The orientation of the device is compared with the magnetic Nord. Therefore it provides absolute orientation. Since the magnetic field is easily interfered with by metal objects inside the building, the accuracy of a magnetometer for indoor navigation is not significantly accurate.

Figure hall effect
Comparison of Magnetometer and Gyroscope
In the experiment described the measurements are extracted from the device rotating on a rectangular track. As can be seen, results acquired from gyroscope are closer to reference values. However, on long straight line intervals one can notice the drift of gyroscope-based angle, while magnetometer provides more accurate results.

Picture “Comparison of magnetic and gyro-based approaches” from this video
Sensor Fusion with Complementary Filter
To minimize drawbacks and compensate for inaccuracy of measurements for gyro- and magnetometer-based heading one can use complementary filter. Measurements from the gyroscope are stable in a short-term period therefore they are used to prohibit sudden orientation changes caused by magnetic errors. Meanwhile, a stable long-term magnetometer trend is used to compensate for the bias of the gyroscope.
Pedestrian Dead Reckoning Algorithm
This algorithm combines heading from the complementary filter and steps from the pedometer algorithm. The goal of PDR is to reconstruct the trajectory of moving human advancing in space with intervals of a length corresponding to estimated step length in direction specified by the angle obtained from the complementary filter.

Picture “Illustration of PDR algorithm” from this video
As one can see, additional errors in position estimation are caused by pedometer, because the length ofstraight sections is longer compared to the reference data.
Conclusion
Inertial navigation allows to provide position of the device, calculate the number of steps produced by a human holding a smartphone or smartwatch and estimate the rotation during the motion. Inertial navigation system algorithms such as pedometer algorithm and complementary filter help to improve the quality of indoor navigation. Repository with Complementary filter, pedometer and other algorithms can be found here.
Discuss more over a private consultation: Link